비지도학습
ML
- 지도학습
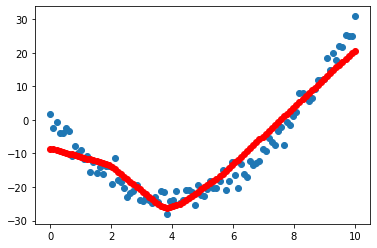
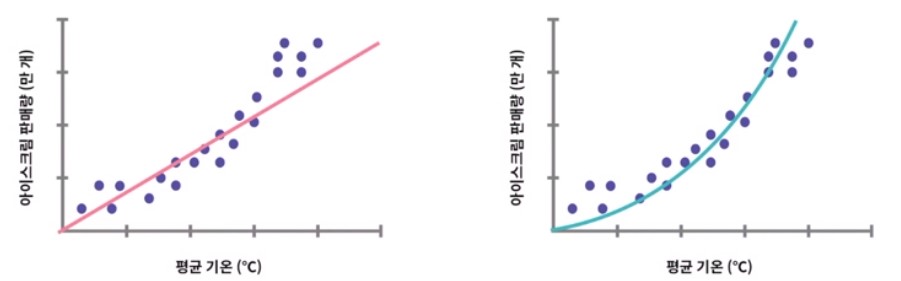
- regression
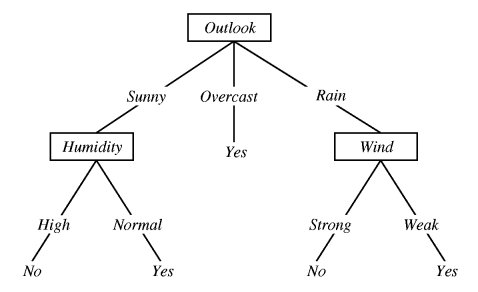
- classification
- 비지도학습
- 차원축소
- 클러스터링
- 강화학습
숨겨진 구조 (hidden structure)
- Hard Clustering
- 데이터 포인트들은 비슷한 것들끼리 뭉쳐있다.
- ex. 강아지 그룹이거나 고양이 그룹이거나, 둘 중 하나.
- 대표 알고리즘: K-means, Hierarchical Clustering
- Soft Clustering
- 한 개의 데이터 포인트는 숨겨진 클러스터들의 결합이다.
- ex. 책 장르 분류 (과학 60% + 역사 40 %)
- 대표 알고리즘: Gaussian Mixture Models (EM, GMM), Soft K-means
Hard Clustering
- 목표: 비슷한 데이터 포인트끼리 모은다.
k: 클러스터 개수, 찾아야 하는 군집 개수
Finding K
- 눈으로 확인
- 모델이 데이터를 얼마나 잘 설명하는가
- 데이터의 특성
- 분석 결과로 얻고자 하는 것 (특정 라벨로 분류, or 분석용인지)
차원축소
데이터들의 여러 특성들을 2차원, 3차원에 나타내기 위해 차원 축소
PCA (Principal Componenet Analysis)
주성분 분석
- 고차원의 데이터를 저차원으로 줄이기 위해 (ex. 시각화)
- 차원이 축소되면서 손실되는 데이터를 줄이는 것이 PCA의 목적
- 데이터 정제 (자주 사용)
클러스터링
주어진 데이터를 비슷한 그룹(클러스터)으로 묶는 알고리즘
몇 개의 그룹으로 묶을 건지 (k 값)은 사람이 줌
K-means
- 중심 (Centroid)
각 클러스터의 “중심”을 의미
- 중심과의 거리 (Distance)
중심과 데이터 포인트와의 거리
Step 1
- 중심 위치 잡기 (랜덤)
- 각각의 데이터 포인트들과 임의로 설정한 중심들에 대해 distance 계산
- distance를 비교하여 이 데이터포인트가 어느 클러스터에 속할지 결정
A 클러스터의 중심과의 거리가 가깝냐, B 클러스터의 중심과의 거리가 가깝냐
Step 2
- 한바퀴 다 돌고 클러스터가 정해지면 중심점을 다시 계산
- 중심점 계산법: 해당 클러스터 내 데ㅣ터 포인트 위치의
무게중심값 (또는 평균)
Step 3
- Step 1과 2를 반복하면 중심점 업데이트
- 어떠한 데이터 포인트의 할당이 변하지 않을 때까지. (중심점을 옮겼는데도 클러스터링이 같게 나올 때)
K-means 구현
wine.csv 데이터를 이용하여 와인들을 clustering 해보기
파일은 아래 텍스트로 첨부
import sklearn.decomposition
import sklearn.cluster
import matplotlib.pyplot as plt
import numpy as np
def main():
X, attributes = input_data() # 파일에서 데이터 읽어오기
X = normalize(X) # x값 정규화 (0~1 사이)
pca, pca_array = run_PCA(X, 2) # 13개의 attributes를 2개로 축소
labels = kmeans(pca_array, 3, [0, 1, 2]) # k=3, 3개의 군집으로 나누기
labels = labels.astype(int)
visualize(pca_array, labels) # 시각화
print(labels)
def input_data():
X = []
attributes = []
with open('wine.csv') as fp:
for line in fp:
X.append([float(x) for x in line.strip().split(',')])
with open('attributes.txt') as fp:
attributes = [x.strip() for x in fp.readlines()]
return np.array(X), attributes
def run_PCA(X, num_components):
pca = sklearn.decomposition.PCA(n_components=num_components)
pca.fit(X)
pca_array = pca.transform(X)
return pca, pca_array
def kmeans(X, num_clusters, initial_centroid_indices):
import time
N = len(X)
centroids = X[initial_centroid_indices]
labels = np.zeros(N)
while True:
is_changed = False # 라벨이 바뀌었는지
for i in range(N):
distances = []
for centroid in centroids:
distances.append(distance(X[i], centroid))
if labels[i] != np.argmin(distances):
is_changed = True
labels[i] = np.argmin(distances) # 클러스터 0, 1, 2 중 하나
# print(labels)
### 새 중심점 계산
for k in range(num_clusters):
x = X[labels == k][:, 0]
y = X[labels == k][:, 1]
x = np.mean(x)
y = np.mean(y)
centroids[k] = [x, y]
if not is_changed:
break
return labels
### 유클리드 거리 norm
def distance(x1, x2):
return np.sqrt(np.sum((x1 - x2) ** 2))
### 정규화
# 0~1사이 값으로 선형
def normalize(X):
for dim in range(len(X[0])):
X[:, dim] -= np.min(X[:, dim])
X[:, dim] /= np.max(X[:, dim])
return X
def visualize(X, labels):
# plt.style.use("ggplot")
plt.figure(figsize=(10, 6))
plt.scatter(X[:, 0], X[:, 1], c=labels)
if __name__ == '__main__':
main()
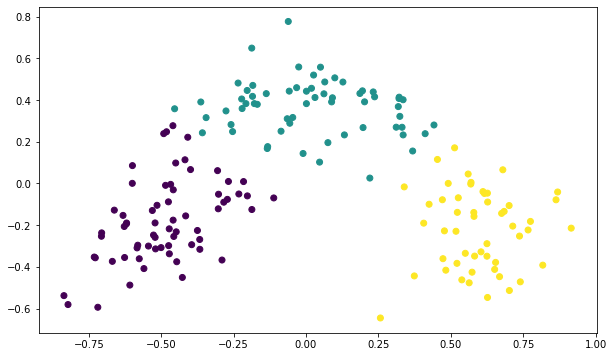
3개의 클러스터로 나눠짐 attributes.csv
Alcohol
Malic acid
Ash
Alcalinity of ash
Magnesium
Total phenols
Flavanoids
Nonflavanoid phenols
Proanthocyanins
Color intensity
Hue
OD280/OD315 of diluted wines
Proline
wine.csv
14.23,1.71,2.43,15.6,127.0,2.8,3.06,0.28,2.29,5.64,1.04,3.92,1065.0
13.2,1.78,2.14,11.2,100.0,2.65,2.76,0.26,1.28,4.38,1.05,3.4,1050.0
13.16,2.36,2.67,18.6,101.0,2.8,3.24,0.3,2.81,5.68,1.03,3.17,1185.0
14.37,1.95,2.5,16.8,113.0,3.85,3.49,0.24,2.18,7.8,0.86,3.45,1480.0
13.24,2.59,2.87,21.0,118.0,2.8,2.69,0.39,1.82,4.32,1.04,2.93,735.0
14.2,1.76,2.45,15.2,112.0,3.27,3.39,0.34,1.97,6.75,1.05,2.85,1450.0
14.39,1.87,2.45,14.6,96.0,2.5,2.52,0.3,1.98,5.25,1.02,3.58,1290.0
14.06,2.15,2.61,17.6,121.0,2.6,2.51,0.31,1.25,5.05,1.06,3.58,1295.0
14.83,1.64,2.17,14.0,97.0,2.8,2.98,0.29,1.98,5.2,1.08,2.85,1045.0
13.86,1.35,2.27,16.0,98.0,2.98,3.15,0.22,1.85,7.22,1.01,3.55,1045.0
14.1,2.16,2.3,18.0,105.0,2.95,3.32,0.22,2.38,5.75,1.25,3.17,1510.0
14.12,1.48,2.32,16.8,95.0,2.2,2.43,0.26,1.57,5.0,1.17,2.82,1280.0
13.75,1.73,2.41,16.0,89.0,2.6,2.76,0.29,1.81,5.6,1.15,2.9,1320.0
14.75,1.73,2.39,11.4,91.0,3.1,3.69,0.43,2.81,5.4,1.25,2.73,1150.0
14.38,1.87,2.38,12.0,102.0,3.3,3.64,0.29,2.96,7.5,1.2,3.0,1547.0
13.63,1.81,2.7,17.2,112.0,2.85,2.91,0.3,1.46,7.3,1.28,2.88,1310.0
14.3,1.92,2.72,20.0,120.0,2.8,3.14,0.33,1.97,6.2,1.07,2.65,1280.0
13.83,1.57,2.62,20.0,115.0,2.95,3.4,0.4,1.72,6.6,1.13,2.57,1130.0
14.19,1.59,2.48,16.5,108.0,3.3,3.93,0.32,1.86,8.7,1.23,2.82,1680.0
13.64,3.1,2.56,15.2,116.0,2.7,3.03,0.17,1.66,5.1,0.96,3.36,845.0
14.06,1.63,2.28,16.0,126.0,3.0,3.17,0.24,2.1,5.65,1.09,3.71,780.0
12.93,3.8,2.65,18.6,102.0,2.41,2.41,0.25,1.98,4.5,1.03,3.52,770.0
13.71,1.86,2.36,16.6,101.0,2.61,2.88,0.27,1.69,3.8,1.11,4.0,1035.0
12.85,1.6,2.52,17.8,95.0,2.48,2.37,0.26,1.46,3.93,1.09,3.63,1015.0
13.5,1.81,2.61,20.0,96.0,2.53,2.61,0.28,1.66,3.52,1.12,3.82,845.0
13.05,2.05,3.22,25.0,124.0,2.63,2.68,0.47,1.92,3.58,1.13,3.2,830.0
13.39,1.77,2.62,16.1,93.0,2.85,2.94,0.34,1.45,4.8,0.92,3.22,1195.0
13.3,1.72,2.14,17.0,94.0,2.4,2.19,0.27,1.35,3.95,1.02,2.77,1285.0
13.87,1.9,2.8,19.4,107.0,2.95,2.97,0.37,1.76,4.5,1.25,3.4,915.0
14.02,1.68,2.21,16.0,96.0,2.65,2.33,0.26,1.98,4.7,1.04,3.59,1035.0
13.73,1.5,2.7,22.5,101.0,3.0,3.25,0.29,2.38,5.7,1.19,2.71,1285.0
13.58,1.66,2.36,19.1,106.0,2.86,3.19,0.22,1.95,6.9,1.09,2.88,1515.0
13.68,1.83,2.36,17.2,104.0,2.42,2.69,0.42,1.97,3.84,1.23,2.87,990.0
13.76,1.53,2.7,19.5,132.0,2.95,2.74,0.5,1.35,5.4,1.25,3.0,1235.0
13.51,1.8,2.65,19.0,110.0,2.35,2.53,0.29,1.54,4.2,1.1,2.87,1095.0
13.48,1.81,2.41,20.5,100.0,2.7,2.98,0.26,1.86,5.1,1.04,3.47,920.0
13.28,1.64,2.84,15.5,110.0,2.6,2.68,0.34,1.36,4.6,1.09,2.78,880.0
13.05,1.65,2.55,18.0,98.0,2.45,2.43,0.29,1.44,4.25,1.12,2.51,1105.0
13.07,1.5,2.1,15.5,98.0,2.4,2.64,0.28,1.37,3.7,1.18,2.69,1020.0
14.22,3.99,2.51,13.2,128.0,3.0,3.04,0.2,2.08,5.1,0.89,3.53,760.0
13.56,1.71,2.31,16.2,117.0,3.15,3.29,0.34,2.34,6.13,0.95,3.38,795.0
13.41,3.84,2.12,18.8,90.0,2.45,2.68,0.27,1.48,4.28,0.91,3.0,1035.0
13.88,1.89,2.59,15.0,101.0,3.25,3.56,0.17,1.7,5.43,0.88,3.56,1095.0
13.24,3.98,2.29,17.5,103.0,2.64,2.63,0.32,1.66,4.36,0.82,3.0,680.0
13.05,1.77,2.1,17.0,107.0,3.0,3.0,0.28,2.03,5.04,0.88,3.35,885.0
14.21,4.04,2.44,18.9,111.0,2.85,2.65,0.3,1.25,5.24,0.87,3.33,1080.0
14.38,3.59,2.28,16.0,102.0,3.25,3.17,0.27,2.19,4.9,1.04,3.44,1065.0
13.9,1.68,2.12,16.0,101.0,3.1,3.39,0.21,2.14,6.1,0.91,3.33,985.0
14.1,2.02,2.4,18.8,103.0,2.75,2.92,0.32,2.38,6.2,1.07,2.75,1060.0
13.94,1.73,2.27,17.4,108.0,2.88,3.54,0.32,2.08,8.9,1.12,3.1,1260.0
13.05,1.73,2.04,12.4,92.0,2.72,3.27,0.17,2.91,7.2,1.12,2.91,1150.0
13.83,1.65,2.6,17.2,94.0,2.45,2.99,0.22,2.29,5.6,1.24,3.37,1265.0
13.82,1.75,2.42,14.0,111.0,3.88,3.74,0.32,1.87,7.05,1.01,3.26,1190.0
13.77,1.9,2.68,17.1,115.0,3.0,2.79,0.39,1.68,6.3,1.13,2.93,1375.0
13.74,1.67,2.25,16.4,118.0,2.6,2.9,0.21,1.62,5.85,0.92,3.2,1060.0
13.56,1.73,2.46,20.5,116.0,2.96,2.78,0.2,2.45,6.25,0.98,3.03,1120.0
14.22,1.7,2.3,16.3,118.0,3.2,3.0,0.26,2.03,6.38,0.94,3.31,970.0
13.29,1.97,2.68,16.8,102.0,3.0,3.23,0.31,1.66,6.0,1.07,2.84,1270.0
13.72,1.43,2.5,16.7,108.0,3.4,3.67,0.19,2.04,6.8,0.89,2.87,1285.0
12.37,0.94,1.36,10.6,88.0,1.98,0.57,0.28,0.42,1.95,1.05,1.82,520.0
12.33,1.1,2.28,16.0,101.0,2.05,1.09,0.63,0.41,3.27,1.25,1.67,680.0
12.64,1.36,2.02,16.8,100.0,2.02,1.41,0.53,0.62,5.75,0.98,1.59,450.0
13.67,1.25,1.92,18.0,94.0,2.1,1.79,0.32,0.73,3.8,1.23,2.46,630.0
12.37,1.13,2.16,19.0,87.0,3.5,3.1,0.19,1.87,4.45,1.22,2.87,420.0
12.17,1.45,2.53,19.0,104.0,1.89,1.75,0.45,1.03,2.95,1.45,2.23,355.0
12.37,1.21,2.56,18.1,98.0,2.42,2.65,0.37,2.08,4.6,1.19,2.3,678.0
13.11,1.01,1.7,15.0,78.0,2.98,3.18,0.26,2.28,5.3,1.12,3.18,502.0
12.37,1.17,1.92,19.6,78.0,2.11,2.0,0.27,1.04,4.68,1.12,3.48,510.0
13.34,0.94,2.36,17.0,110.0,2.53,1.3,0.55,0.42,3.17,1.02,1.93,750.0
12.21,1.19,1.75,16.8,151.0,1.85,1.28,0.14,2.5,2.85,1.28,3.07,718.0
12.29,1.61,2.21,20.4,103.0,1.1,1.02,0.37,1.46,3.05,0.906,1.82,870.0
13.86,1.51,2.67,25.0,86.0,2.95,2.86,0.21,1.87,3.38,1.36,3.16,410.0
13.49,1.66,2.24,24.0,87.0,1.88,1.84,0.27,1.03,3.74,0.98,2.78,472.0
12.99,1.67,2.6,30.0,139.0,3.3,2.89,0.21,1.96,3.35,1.31,3.5,985.0
11.96,1.09,2.3,21.0,101.0,3.38,2.14,0.13,1.65,3.21,0.99,3.13,886.0
11.66,1.88,1.92,16.0,97.0,1.61,1.57,0.34,1.15,3.8,1.23,2.14,428.0
13.03,0.9,1.71,16.0,86.0,1.95,2.03,0.24,1.46,4.6,1.19,2.48,392.0
11.84,2.89,2.23,18.0,112.0,1.72,1.32,0.43,0.95,2.65,0.96,2.52,500.0
12.33,0.99,1.95,14.8,136.0,1.9,1.85,0.35,2.76,3.4,1.06,2.31,750.0
12.7,3.87,2.4,23.0,101.0,2.83,2.55,0.43,1.95,2.57,1.19,3.13,463.0
12.0,0.92,2.0,19.0,86.0,2.42,2.26,0.3,1.43,2.5,1.38,3.12,278.0
12.72,1.81,2.2,18.8,86.0,2.2,2.53,0.26,1.77,3.9,1.16,3.14,714.0
12.08,1.13,2.51,24.0,78.0,2.0,1.58,0.4,1.4,2.2,1.31,2.72,630.0
13.05,3.86,2.32,22.5,85.0,1.65,1.59,0.61,1.62,4.8,0.84,2.01,515.0
11.84,0.89,2.58,18.0,94.0,2.2,2.21,0.22,2.35,3.05,0.79,3.08,520.0
12.67,0.98,2.24,18.0,99.0,2.2,1.94,0.3,1.46,2.62,1.23,3.16,450.0
12.16,1.61,2.31,22.8,90.0,1.78,1.69,0.43,1.56,2.45,1.33,2.26,495.0
11.65,1.67,2.62,26.0,88.0,1.92,1.61,0.4,1.34,2.6,1.36,3.21,562.0
11.64,2.06,2.46,21.6,84.0,1.95,1.69,0.48,1.35,2.8,1.0,2.75,680.0
12.08,1.33,2.3,23.6,70.0,2.2,1.59,0.42,1.38,1.74,1.07,3.21,625.0
12.08,1.83,2.32,18.5,81.0,1.6,1.5,0.52,1.64,2.4,1.08,2.27,480.0
12.0,1.51,2.42,22.0,86.0,1.45,1.25,0.5,1.63,3.6,1.05,2.65,450.0
12.69,1.53,2.26,20.7,80.0,1.38,1.46,0.58,1.62,3.05,0.96,2.06,495.0
12.29,2.83,2.22,18.0,88.0,2.45,2.25,0.25,1.99,2.15,1.15,3.3,290.0
11.62,1.99,2.28,18.0,98.0,3.02,2.26,0.17,1.35,3.25,1.16,2.96,345.0
12.47,1.52,2.2,19.0,162.0,2.5,2.27,0.32,3.28,2.6,1.16,2.63,937.0
11.81,2.12,2.74,21.5,134.0,1.6,0.99,0.14,1.56,2.5,0.95,2.26,625.0
12.29,1.41,1.98,16.0,85.0,2.55,2.5,0.29,1.77,2.9,1.23,2.74,428.0
12.37,1.07,2.1,18.5,88.0,3.52,3.75,0.24,1.95,4.5,1.04,2.77,660.0
12.29,3.17,2.21,18.0,88.0,2.85,2.99,0.45,2.81,2.3,1.42,2.83,406.0
12.08,2.08,1.7,17.5,97.0,2.23,2.17,0.26,1.4,3.3,1.27,2.96,710.0
12.6,1.34,1.9,18.5,88.0,1.45,1.36,0.29,1.35,2.45,1.04,2.77,562.0
12.34,2.45,2.46,21.0,98.0,2.56,2.11,0.34,1.31,2.8,0.8,3.38,438.0
11.82,1.72,1.88,19.5,86.0,2.5,1.64,0.37,1.42,2.06,0.94,2.44,415.0
12.51,1.73,1.98,20.5,85.0,2.2,1.92,0.32,1.48,2.94,1.04,3.57,672.0
12.42,2.55,2.27,22.0,90.0,1.68,1.84,0.66,1.42,2.7,0.86,3.3,315.0
12.25,1.73,2.12,19.0,80.0,1.65,2.03,0.37,1.63,3.4,1.0,3.17,510.0
12.72,1.75,2.28,22.5,84.0,1.38,1.76,0.48,1.63,3.3,0.88,2.42,488.0
12.22,1.29,1.94,19.0,92.0,2.36,2.04,0.39,2.08,2.7,0.86,3.02,312.0
11.61,1.35,2.7,20.0,94.0,2.74,2.92,0.29,2.49,2.65,0.96,3.26,680.0
11.46,3.74,1.82,19.5,107.0,3.18,2.58,0.24,3.58,2.9,0.75,2.81,562.0
12.52,2.43,2.17,21.0,88.0,2.55,2.27,0.26,1.22,2.0,0.9,2.78,325.0
11.76,2.68,2.92,20.0,103.0,1.75,2.03,0.6,1.05,3.8,1.23,2.5,607.0
11.41,0.74,2.5,21.0,88.0,2.48,2.01,0.42,1.44,3.08,1.1,2.31,434.0
12.08,1.39,2.5,22.5,84.0,2.56,2.29,0.43,1.04,2.9,0.93,3.19,385.0
11.03,1.51,2.2,21.5,85.0,2.46,2.17,0.52,2.01,1.9,1.71,2.87,407.0
11.82,1.47,1.99,20.8,86.0,1.98,1.6,0.3,1.53,1.95,0.95,3.33,495.0
12.42,1.61,2.19,22.5,108.0,2.0,2.09,0.34,1.61,2.06,1.06,2.96,345.0
12.77,3.43,1.98,16.0,80.0,1.63,1.25,0.43,0.83,3.4,0.7,2.12,372.0
12.0,3.43,2.0,19.0,87.0,2.0,1.64,0.37,1.87,1.28,0.93,3.05,564.0
11.45,2.4,2.42,20.0,96.0,2.9,2.79,0.32,1.83,3.25,0.8,3.39,625.0
11.56,2.05,3.23,28.5,119.0,3.18,5.08,0.47,1.87,6.0,0.93,3.69,465.0
12.42,4.43,2.73,26.5,102.0,2.2,2.13,0.43,1.71,2.08,0.92,3.12,365.0
13.05,5.8,2.13,21.5,86.0,2.62,2.65,0.3,2.01,2.6,0.73,3.1,380.0
11.87,4.31,2.39,21.0,82.0,2.86,3.03,0.21,2.91,2.8,0.75,3.64,380.0
12.07,2.16,2.17,21.0,85.0,2.6,2.65,0.37,1.35,2.76,0.86,3.28,378.0
12.43,1.53,2.29,21.5,86.0,2.74,3.15,0.39,1.77,3.94,0.69,2.84,352.0
11.79,2.13,2.78,28.5,92.0,2.13,2.24,0.58,1.76,3.0,0.97,2.44,466.0
12.37,1.63,2.3,24.5,88.0,2.22,2.45,0.4,1.9,2.12,0.89,2.78,342.0
12.04,4.3,2.38,22.0,80.0,2.1,1.75,0.42,1.35,2.6,0.79,2.57,580.0
12.86,1.35,2.32,18.0,122.0,1.51,1.25,0.21,0.94,4.1,0.76,1.29,630.0
12.88,2.99,2.4,20.0,104.0,1.3,1.22,0.24,0.83,5.4,0.74,1.42,530.0
12.81,2.31,2.4,24.0,98.0,1.15,1.09,0.27,0.83,5.7,0.66,1.36,560.0
12.7,3.55,2.36,21.5,106.0,1.7,1.2,0.17,0.84,5.0,0.78,1.29,600.0
12.51,1.24,2.25,17.5,85.0,2.0,0.58,0.6,1.25,5.45,0.75,1.51,650.0
12.6,2.46,2.2,18.5,94.0,1.62,0.66,0.63,0.94,7.1,0.73,1.58,695.0
12.25,4.72,2.54,21.0,89.0,1.38,0.47,0.53,0.8,3.85,0.75,1.27,720.0
12.53,5.51,2.64,25.0,96.0,1.79,0.6,0.63,1.1,5.0,0.82,1.69,515.0
13.49,3.59,2.19,19.5,88.0,1.62,0.48,0.58,0.88,5.7,0.81,1.82,580.0
12.84,2.96,2.61,24.0,101.0,2.32,0.6,0.53,0.81,4.92,0.89,2.15,590.0
12.93,2.81,2.7,21.0,96.0,1.54,0.5,0.53,0.75,4.6,0.77,2.31,600.0
13.36,2.56,2.35,20.0,89.0,1.4,0.5,0.37,0.64,5.6,0.7,2.47,780.0
13.52,3.17,2.72,23.5,97.0,1.55,0.52,0.5,0.55,4.35,0.89,2.06,520.0
13.62,4.95,2.35,20.0,92.0,2.0,0.8,0.47,1.02,4.4,0.91,2.05,550.0
12.25,3.88,2.2,18.5,112.0,1.38,0.78,0.29,1.14,8.21,0.65,2.0,855.0
13.16,3.57,2.15,21.0,102.0,1.5,0.55,0.43,1.3,4.0,0.6,1.68,830.0
13.88,5.04,2.23,20.0,80.0,0.98,0.34,0.4,0.68,4.9,0.58,1.33,415.0
12.87,4.61,2.48,21.5,86.0,1.7,0.65,0.47,0.86,7.65,0.54,1.86,625.0
13.32,3.24,2.38,21.5,92.0,1.93,0.76,0.45,1.25,8.42,0.55,1.62,650.0
13.08,3.9,2.36,21.5,113.0,1.41,1.39,0.34,1.14,9.4,0.57,1.33,550.0
13.5,3.12,2.62,24.0,123.0,1.4,1.57,0.22,1.25,8.6,0.59,1.3,500.0
12.79,2.67,2.48,22.0,112.0,1.48,1.36,0.24,1.26,10.8,0.48,1.47,480.0
13.11,1.9,2.75,25.5,116.0,2.2,1.28,0.26,1.56,7.1,0.61,1.33,425.0
13.23,3.3,2.28,18.5,98.0,1.8,0.83,0.61,1.87,10.52,0.56,1.51,675.0
12.58,1.29,2.1,20.0,103.0,1.48,0.58,0.53,1.4,7.6,0.58,1.55,640.0
13.17,5.19,2.32,22.0,93.0,1.74,0.63,0.61,1.55,7.9,0.6,1.48,725.0
13.84,4.12,2.38,19.5,89.0,1.8,0.83,0.48,1.56,9.01,0.57,1.64,480.0
12.45,3.03,2.64,27.0,97.0,1.9,0.58,0.63,1.14,7.5,0.67,1.73,880.0
14.34,1.68,2.7,25.0,98.0,2.8,1.31,0.53,2.7,13.0,0.57,1.96,660.0
13.48,1.67,2.64,22.5,89.0,2.6,1.1,0.52,2.29,11.75,0.57,1.78,620.0
12.36,3.83,2.38,21.0,88.0,2.3,0.92,0.5,1.04,7.65,0.56,1.58,520.0
13.69,3.26,2.54,20.0,107.0,1.83,0.56,0.5,0.8,5.88,0.96,1.82,680.0
12.85,3.27,2.58,22.0,106.0,1.65,0.6,0.6,0.96,5.58,0.87,2.11,570.0
12.96,3.45,2.35,18.5,106.0,1.39,0.7,0.4,0.94,5.28,0.68,1.75,675.0
13.78,2.76,2.3,22.0,90.0,1.35,0.68,0.41,1.03,9.58,0.7,1.68,615.0
13.73,4.36,2.26,22.5,88.0,1.28,0.47,0.52,1.15,6.62,0.78,1.75,520.0
13.45,3.7,2.6,23.0,111.0,1.7,0.92,0.43,1.46,10.68,0.85,1.56,695.0
12.82,3.37,2.3,19.5,88.0,1.48,0.66,0.4,0.97,10.26,0.72,1.75,685.0
13.58,2.58,2.69,24.5,105.0,1.55,0.84,0.39,1.54,8.66,0.74,1.8,750.0
13.4,4.6,2.86,25.0,112.0,1.98,0.96,0.27,1.11,8.5,0.67,1.92,630.0
12.2,3.03,2.32,19.0,96.0,1.25,0.49,0.4,0.73,5.5,0.66,1.83,510.0
12.77,2.39,2.28,19.5,86.0,1.39,0.51,0.48,0.64,9.899999,0.57,1.63,470.0
14.16,2.51,2.48,20.0,91.0,1.68,0.7,0.44,1.24,9.7,0.62,1.71,660.0
13.71,5.65,2.45,20.5,95.0,1.68,0.61,0.52,1.06,7.7,0.64,1.74,740.0
13.4,3.91,2.48,23.0,102.0,1.8,0.75,0.43,1.41,7.3,0.7,1.56,750.0
13.27,4.28,2.26,20.0,120.0,1.59,0.69,0.43,1.35,10.2,0.59,1.56,835.0
13.17,2.59,2.37,20.0,120.0,1.65,0.68,0.53,1.46,9.3,0.6,1.62,840.0
14.13,4.1,2.74,24.5,96.0,2.05,0.76,0.56,1.35,9.2,0.61,1.6,560.0
Scikit-learn 활용
import pandas as pd
import numpy as np
from sklearn.cluster import KMeans
from sklearn.datasets import load_iris
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
def load_data():
iris = load_iris()
irisDF = pd.DataFrame(data = iris.data, columns = iris.feature_names)
irisDF['target'] = iris.target
return irisDF
def k_means_clus(irisDF):
kmeans = KMeans(init="random", n_clusters=3, random_state=100)
kmeans.fit(irisDF)
irisDF['cluster'] = kmeans.labels_
# 군집화 결과를 보기 위해 groupby 함수를 사용해보겠습니다.
iris_result = irisDF.groupby(['target','cluster'])['sepal length (cm)'].count()
print(iris_result)
return iris_result, irisDF
# 군집화 결과 시각화하기
def Visualize(irisDF):
pca = PCA(n_components=2)
pca_transformed = pca.fit_transform(irisDF)
irisDF['pca_x'] = pca_transformed[:,0]
irisDF['pca_y'] = pca_transformed[:,1]
# 군집된 값이 0, 1, 2 인 경우, 인덱스 추출
idx_0 = irisDF[irisDF['cluster'] == 0].index
idx_1 = irisDF[irisDF['cluster'] == 1].index
idx_2 = irisDF[irisDF['cluster'] == 2].index
# 각 군집 인덱스의 pca_x, pca_y 값 추출 및 시각화
fig, ax = plt.subplots()
ax.scatter(x=irisDF.loc[idx_0, 'pca_x'], y= irisDF.loc[idx_0, 'pca_y'], marker = 'o')
ax.scatter(x=irisDF.loc[idx_1, 'pca_x'], y= irisDF.loc[idx_1, 'pca_y'], marker = 's')
ax.scatter(x=irisDF.loc[idx_2, 'pca_x'], y= irisDF.loc[idx_2, 'pca_y'], marker = '^')
ax.set_title('K-menas')
ax.set_xlabel('PCA1')
ax.set_ylabel('PCA2')
fig.savefig("plot.png")
def main():
irisDF = load_data()
iris_result, irisDF = k_means_clus(irisDF)
Visualize(irisDF)
if __name__ == "__main__":
main()