Basic | Simple Linear Regression
in Machine Learning / Basic
선형 회귀에 대하여, 그리고 python과 사이킷런으로 단순선형회귀모델 구현하기
Regression 이란
regression = 추세선
ML 분류
- 지도학습
- regression
- linear regression
- 단순 선형회귀
- 다중 회귀분석
- 다항 회귀분석
- logistic regression
- K-Nearest Neightbors regression
- Decision Tree
- classification
- 비지도학습
- 강화학습
지도 학습 중 하나로, 입력값에 따른 미래 결과값을 예측하는 알고리즘
ex. 몸무게-키 데이터에서 몸무게에 따른 키 예측하기
Simple Linear Regression
단순 선형 회귀
- 하나의 X (input) -> Y (output) 예측
- 직선 하나
- 기울기(\(\beta_1\))와 절편(\(\beta_0\)) 찾기
선형회귀의 목적: \(Y = \beta_0 + \beta_1X\) 의 직선 찾기
좋은 직선 긋기, Loss Function
좋은 직선이란? 실제값(y)과 예측값(\(\beta_0X + \beta_1\) )의 차이가 적을수록 좋다.
실제값: input에 대한 실제 output
예측값: input에 대한 예측값, 직선에 x를 넣었을 때 나오는 값
Loss Function (손실함수) \[\sum_{i}^n (y_i - (\beta_0 + \beta_1x_i))^2\]
- = Cost Funtion
- loss = 예측값과 실제값의 차이
- 기계학습을 통해 결국 최소로 만들고자 하는 것,학습은 loss를 줄이는 방향으로 진행된다.
차이를 제곱해서 더하는 이유: 차이가 음수, 양수 모두 존재한다면 전체 차이를 구하기 위해 모두 더할 때 음수, 양수 차이가 상쇄 되어 버린다. -> 실제로는 차이가 많이 나도 전체 차이는 0이 나올 수도 있다
좋은 직선, beta 값을 찾는 법
Gradient Descent (경사하강법)
- loss function을 최소로 만드는 \(\beta_0 \beta_1\) 찾기
- 현재 위치에서 기울기가 가장 낮은 쪽으로 이동
- 현재 위치에서 기울기(미분값, 경사)를 구하고 경사의 반대 방향으로 이동시키면 극값이 나온다.
- 경사의 반대 방향 의미: 어떤 점에서 기울기가 양수라면 우상향 그래프, 최솟값으로 가기 위해서는 왼쪽(음수 방향)으로 이동해야 하고, 기울기가 음수라면 우하향 그래프이므로 최솟값으로 오른쪽(양수 방향)으로 이동해야 한다.
- 다음 점 위치:
지역 최적해로 수렴, 전역 최적해 보장 X
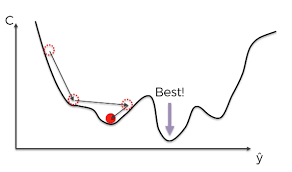
출처: 리브레 위키
Scikit-learn을 이용한 회귀분석
import matplotlib.pyplot as plt
import numpy as np
from sklearn.linear_model import LinearRegression
# loss function 구현
def loss(x, y, beta_0, beta_1):
N = len(x)
l = 0 # loss 값
for i in range(N):
l += (y[i] - (beta_0 + beta_1*x[i]))**2
return l
# sample data
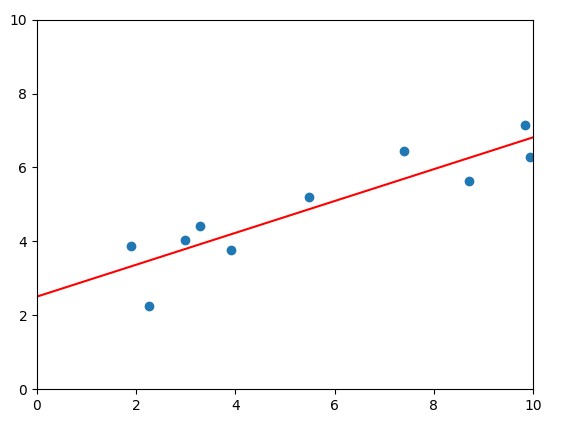
X = [8.70153760, 3.90825773, 1.89362433, 3.28730045, 7.39333004, 2.98984649, 2.25757240, 9.84450732, 9.94589513, 5.48321616]
Y = [5.64413093, 3.75876583, 3.87233310, 4.40990425, 6.43845020, 4.02827829, 2.26105955, 7.15768995, 6.29097441, 5.19692852]
train_X = np.array(X).reshape(-1, 1) # 10x1로 reshape
train_Y = np.array(Y).reshape(-1, 1)
###########
### 모델 객체 생성 및 train
lrmodel = LinearRegression()
lrmodel.fit(train_X, train_Y)
beta_0 = lrmodel.intercept_ # lrmodel로 구한 직선의 y절편
beta_1 = lrmodel.coef_[0] # lrmodel로 구한 직선의 기울기
###########
### 학습 결과 출력
print("beta_0: %f" % beta_0)
print("beta_1: %f" % beta_1)
print("Loss: %f" % loss(X, Y, beta_0, beta_1))
plt.scatter(X, Y)
plt.plot([0, 10], [beta_0, 10 * beta_1 + beta_0], c='r')
plt.xlim(0, 10) # 그래프의 X축을 설정합니다.
plt.ylim(0, 10) # 그래프의 Y축을 설정합니다.
Reference
https://karupro.tistory.com/99 https://brunch.co.kr/@mnc/9 https://librewiki.net/wiki/%EA%B2%BD%EC%82%AC%ED%95%98%EA%B0%95%EB%B2%95