Basic | Multiple Linear, Polynomial Regression
다중 선형회귀와 다항 회귀 그리고 과적합 방지
Multiple Linear Regression
다중 선형 회귀
- 여러 개의 X (input) -> Y (output) 예측
- 직선 하나
- 직선 방정식: \(Y = \beta_0 + \beta_1X_1 + \beta_2X_2 + ... + \beta_iX_i\)
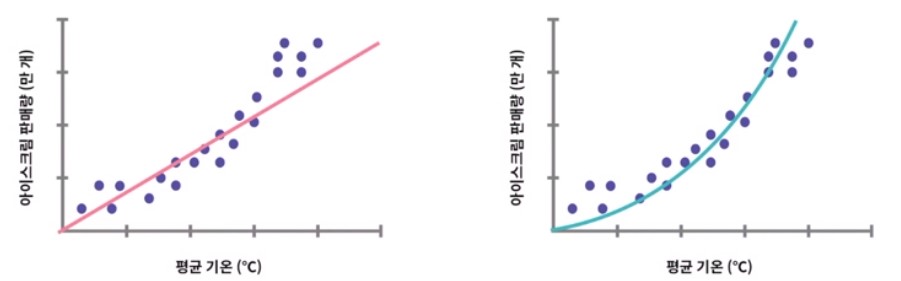
- 애초에 데이터들의 관계가 선형적이지 않다면? (아래와 같이)
출처: elice
-> 다항회귀의 필요성
Polynomial Regression
다항 회귀
- 1차 함수 선형식으로 표현하기 어려운 분포의 데이터를 위한 회귀 (곡선)
- 다항 회귀식: \(Y = \beta_0 + \beta_1X_1 + \beta_2X_2^2 + ... + \beta_iX_i^i\)
다항 회귀 원리
- 기존 입력값 \(X_i\)를 전처리한 새로운 변수를 추가시켜 선형 회귀 모델로 예측
선형회귀모델을 사용하는 것은 동일, X의 전처리가 중요함 - 예를 들어, \(Y = \beta_0 + \beta_1X_1 + \beta_2X_1^2\) 에서 전처리된 새로운 변수 \(X_1^2\)를 \(X_2\)로 치환하면
- \(Y = \beta_0 + \beta_1X_1 + \beta_2X_2\) 의 다중 선형회귀 식과 같다.
다항 회귀 특징
- 일차 함수식으로 표현할 수 없는 복잡한 데이터 분포에도 적용 가능
- 과적합1 현상 발생 가능성
Scikit-learn을 이용한 다중회귀 구현
fetch_california_housing 데이터를 이용해서 다중 회귀 분석을 구현해보고 모델의 점수를 매겨보자.
fetch_california_housing: scikit learn 라이브러리에서 지원하는 데이터셋 중 하나, California housing price 데이터 파이썬 구현 코드
import matplotlib.pyplot as plt
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
# fetch_california_housing 데이터 가져오기
from sklearn.datasets import fetch_california_housing
def load_data():
X, y = fetch_california_housing(return_X_y = True)
print("데이터의 입력값(X)의 개수 :", X.shape[1])
# train-test 데이터 나누기 (8:2)
train_X, test_X, train_y, test_y = train_test_split(X, y, test_size=0.2, random_state=123)
return train_X, test_X, train_y, test_y
# regression 모델 생성, 학습
def Multi_Regression(train_X,train_y):
multilinear = LinearRegression()
multilinear.fit(train_X, train_y)
return multilinear
def main():
train_X, test_X, train_y, test_y = load_data()
# 모델 생성, 학습
multilinear = Multi_Regression(train_X,train_y)
# 학습된 모델로 테스트 데이터에 대해 예측하기
predicted = multilinear.predict(test_X)
model_score = multilinear.score(test_X, test_y)
print("\n> 모델 평가 점수 :", model_score)
beta_0 = multilinear.intercept_
beta_i_list = multilinear.coef_
print("\n> beta_0 : ",beta_0)
print("> beta_i_list : ",beta_i_list)
return predicted, beta_0, beta_i_list, model_score
if __name__ == "__main__":
main()
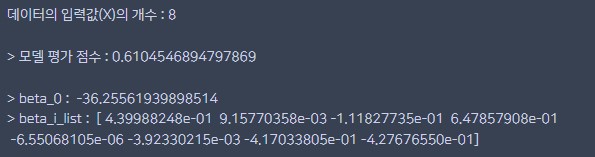
실행 결과
과적합 방지
1. 교차 검증 (Cross Validation)
- train / test / valiation 으로 데이터 나누기
k-fold교차 검증을 많이 사용함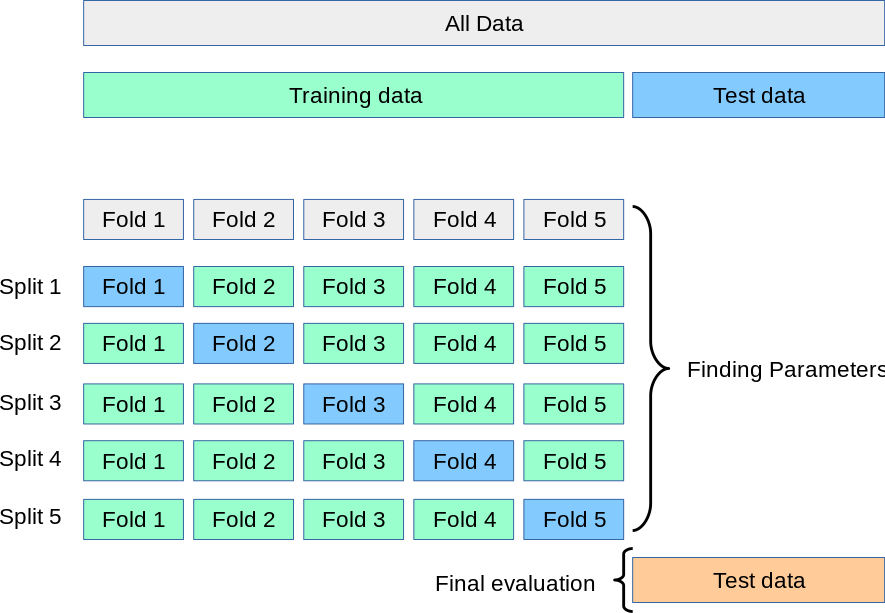
출처: Scikit-learn
k-fold validation 방식
- 훈련 데이터를 계속 변경하여 학습시킴 (특정 데이터에 지나치게 과적합 되는 것을 방지)
- 데이터 셋을 K개로 나눔
- K중 한 개를 검증용, 나머지를 훈련용으로 사용
- K개 모델의 평균 성능이 최종 모델 성능
- test data는 무조건 고정, 학습에 사용하지 않음
2. 정규화 (Regularization)
모델의 복잡성을 줄여 일반화를 증가시키자. 파라미터 \(\beta\) 의 개수를 줄이자
선형 회귀를 위한 정규화 방법
- L1 정규화 (Lasso)
- L2 정규화 (Ridge)
Reference
- https://www.geeksforgeeks.org/multiple-linear-regression-with-scikit-learn/
- https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.KFold.html
과도하게 학습 데이터에 맞춰져 일반화 능력이 떨어지는 상태, 학습 데이터에 대해서는 오차가 감소하지만 실제 데이터에 대해서는 오차가 증가하게 된다. ↩︎