Basic | 지도학습 분류 알고리즘 - Decision Tree

in Machine Learning / Basic

의사결정나무를 이용하여 binary classifier 만들기

Decision Tree

의사결정트리

예시
OUTLOOK, Temperature, HUMIDITY, WINDY 네 가지 attribute에 따라 테니스 경기 Play/Don’t Play에 대한 기록이 아래와 같다.

출처: nulpointerexception.com

그렇다면 각 attribute의 값이 Sunny, Cool, Normal, True 일 때 테니스 경기를 할까 말까? 위의 테이블 데이터를 바탕으로 decision tree를 만들면 아래와 같다.

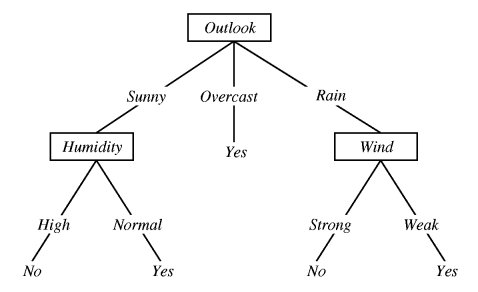
출처: nulpointerexception.com

출처: imgur, Humdity 부분이 가지가 반대로 되어 있는 점 참고

마치 스무고개처럼 동작하는데, 위의 의사결정 트리에 따르면 Sunny, Cool, Normal, True의 경우 테니스 경기를 play할 것이라고 예측할 수 있다.

언제 Decision Tree를 사용하는가.

  • attribute에 대한 값이 pair 형태일 때 (ex. Wind: Strong / Weak)
  • 예측해야 하는 타겟 값이 명확할 때 (Play?: Yes / No)
  • 훈련용 데이터에 손실이 있거나 에러가 있을 수 있을 때 (Decision Tree는 다수결로 동작하기 때문에 데이터 손실이나 에러에 상대적으로 강함)

=> 물론 분류(classification) 뿐만 아니라 회귀(regression)에도 Decision Tree를 사용할 수 있다.

불순도/불확실성

Decision Tree가 만들어지면 node를 따라 내려가면서 값을 예측하는 건 이제 알겠고, 그럼 Decision Tree는 어떻게 만드는 걸까? 나무가지가 나눠지는 분기 기준을 어떻게 세우는 걸까?

불순도(impurity)가 최대한 감소하는 방향으로 학습을 진행하여 Decision Tree를 만든다.


불순도를 나타내는 대표적인 지표에는 Entropy와 Gini Index가 있다. 계산 방법은 아래와 같고, Tree의 한 node 범주로 분류되는 데이터들이 얼마나 비슷한지에 대한 값이라고 생각하면 된다. 예를 들면, Tennis에서 Outlook-Overcast 루트로 분류되는 4개의 데이터(위의 데이터 테이블 참고)가 모두 Yes 값이므로 불순도가 0이다. (Entropy: 0) 반면 Outlook-Sunny 루트로 분류되는 5개의 데이터의 경우 Yes가 2개 No가 3개이므로 불순도가 높다. (Entropy: 0.97)

Entropy
\(Entropy(A)=-\sum _{ k=1 }^{ m }{ { p }_{ k }\log _{ 2 }{ { (p }_{ k }) } }\)

Gini Index (지니 계수)
\(G.I(A)=\sum _{ i=1 }^{ d }{ { \left( { R }_{ i }\left( 1-\sum _{ k=1 }^{ m }{ { p }_{ ik }^{ 2 } } \right) \right) } }\)

두 지표의 가장 큰 차이점: 불순도가 가장 낮을 때 (모든 데이터 값이 동일할 때)는 Entropy: 0, Gini Index: 0이지만, 불순도가 가장 높을 때 (예를 들어 이진분류에서 반반씩 섞여 있는 경우) Entropy: 1, Gini Index: 0.5이다.

Decision Tree 학습 과정

재귀적 분기(Recursive Partitioning)과 가지치기(Prunning)이 이루어진다.

  1. 임의로 attribute를 하나 골라 분할한다고(분기) 가정한 후, 위의 지표값 중 하나를 선택하여 계산한다.
  2. (분기 전의 불순도 - 분기 후의 불순도) = 정보 획득(Information Gain)을 계산한다.
  3. 정보 획득이 가장 큰 변수(attribute)와 그 지점(value 혹은 범위)를 선택하여 분기
  4. 불순도가 0이 되거나 leaf node의 데이터 개수가 특정 개 미만이 될때까지 반복한다. 재귀적 분기(Recursive Partitioning)
  5. tree의 깊이가 너무 깊어지면 overfitting이 발생할 수 있으므로, 가지치기(prunning)을 통해 여러 분기를 통합시킬 수 있다.

대충 다양한 기준으로 나눠보고 최대한 균일하게 나뉘는 기준을 선택한다는 뜻, brute force와 느낌이 비슷하다.

Decision Tree 특징

  • 계산복잡성 대비 높은 에측 성능
  • 변수 단위 설명력 높음 (왜 이런 결과가 나왔는지 tree 시각적 확인 가능)
  • decision boundary가 데이터 축에 수직이기 때문에 특정 데이터에만 잘 작동할 가능성이 높다.

    이를 해결하기 위해 random forest1 모델을 활용할 수 있다.

Scikit-learn 모델 활용

파이썬 코드 
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

from elice_utils import EliceUtils
elice_utils = EliceUtils()

def load_data():
    
    X, y = load_iris(return_X_y = True) 
    
    train_X, test_X, train_y, test_y = train_test_split(X, y, test_size=0.2, random_state=100)
    
    return train_X, test_X, train_y, test_y


def main():
    
    train_X, test_X, train_y, test_y = load_data()
    
    clf = DecisionTreeClassifier() # 분류기(classifier) 정의
    
    clf.fit(train_X, train_y) # 분류기 학습
    
    pred = clf.predict(test_X) # test_x 값에 대한 예측값 생성

    print('정확도 : {0:.4f}'.format(accuracy_score(test_y, pred)))
    
    return pred
    
if __name__ == "__main__":
    main()


Reference

  • https://ratsgo.github.io/machine%20learning/2017/03/26/tree/
  • https://nulpointerexception.com/2017/12/16/a-tutorial-to-understand-decision-tree-id3-learning-algorithm/

  1. Decision Tree를 여러개 만들어 결과를 종합하여 예측 성능을 높이는 기법 (앙상블 - Bagging) ↩︎